В математике существует много правил и законов, которые мы учимся ещё в школе. Одно из них гласит: нельзя делить на ноль. Но почему? Ведь на первый взгляд это кажется довольно странным ограничением. Не все знают, но деление на ноль ведёт к множеству проблем, которые противоречат основным правилам и логике математики.
Самое главное объяснение можно найти в самом определении деления. Если мы делим число A на число B, то ищем такое число C, что C * B = A. Однако, если в качестве B мы выберем ноль, то у нас не получится найти такое число C. В математической терминологии говорят, что деление на ноль не имеет смысла. Именно поэтому это действие запрещено.
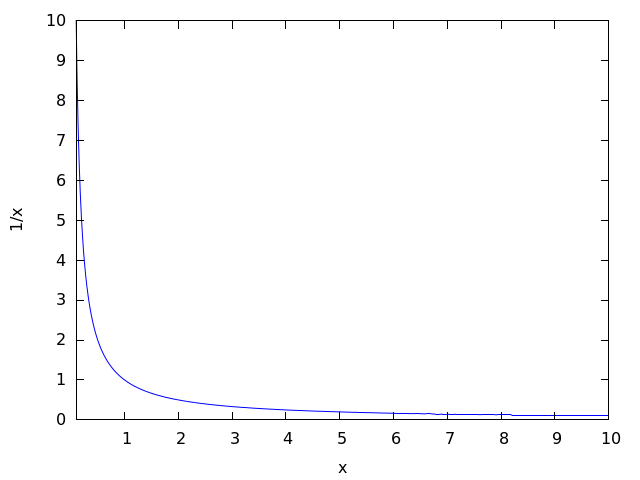
Другое важное замечание связано с самим понятием бесконечности. Если мы поделим число на очень маленькое число, то получим очень большое значение. Но если мы поделим число на ноль, то получим бесконечность. И в математике бесконечность – это неопределённость, с которой трудно работать. Отсюда следует, что деление на ноль приводит к неясной и неопределённой ситуации, которую сложно анализировать и использовать в вычислениях.
Вредительство деления на ноль
Деление на ноль нарушает основные математические правила и приводит к некорректным результатам. Попытка разделить число на ноль приводит к появлению бесконечно больших чисел и неопределенностям. Более того, деление на ноль может привести к сбоям компьютерных программ и ошибкам в вычислениях.
Одна из основных причин, почему нельзя делить на ноль, заключается в том, что ноль не имеет обратного значения. В математике и программировании обратное значение числа получается путем умножения на обратный элемент. Ноль не имеет обратного элемента, поэтому вопрос о делении числа на ноль остается без ответа.
Деление на ноль также приводит к проблемам в алгоритмах и вычислениях. Многие вычислительные задачи требуют использования деления, и любая ошибка в этих вычислениях может привести к непредсказуемым результатам. Кроме того, деление на ноль может вызвать ошибку в работе программы и привести к аварийному завершению.
В итоге, деление на ноль является недопустимой операцией, которая не имеет смысла и приводит к ошибкам и неопределенностям. Чтобы избежать проблем и обеспечить корректную работу математических операций, необходимо строго соблюдать правила и отказаться от попыток деления на ноль.
Последствия деления на ноль
Одна из основных причин, почему деление на ноль невозможно, связана с математическими правилами и определениями. В математике существует понятие «неопределенности», и деление на ноль относится к этой категории. Ноль не может быть использован в качестве делителя, потому что результатом такой операции будет неопределенное значение, которое не имеет смысла в контексте числового выражения.
Последствия деления на ноль могут быть серьезными и привести к некорректным результатам или ошибкам в программировании, научных расчетах, физических и финансовых моделях. Примерами таких ошибок могут быть деление стоимости на количество товаров, деление скорости на время, деление энергии на массу и т.д.
Ошибки, связанные с делением на ноль, могут негативно повлиять на работу программ и систем, привести к сбоям и потере данных. Поэтому программисты и математики стремятся избегать деления на ноль и обрабатывать эту ситуацию в коде, чтобы предотвратить возможные проблемы.
Уничтожение математического порядка
В математике существуют различные законы и правила, которые определяют порядок операций. Например, сначала выполняются операции умножения и деления, затем — сложения и вычитания. Этот порядок позволяет получать правильные и однозначные результаты вычислений.
Когда мы пытаемся разделить число на ноль, нарушается этот математический порядок. Возникает ситуация, когда нет однозначного решения, так как неопределенность присутствует в самом делении на ноль. Результат становится неопределенным и не имеет смысла в контексте математики.
Кроме того, деление на ноль противоречит самому понятию деления. Деление — это разделение одного числа на другое для определения, сколько раз второе число содержится в первом. Но если мы делим на ноль, мы пытаемся разделить число на «ничто». Это не имеет смысла и противоречит основам математики.
В связи со всем вышеизложенным, деление на ноль считается недопустимым и не определенным в математике. Поэтому во всех вычислениях и формулах мы должны избегать таких операций, чтобы сохранить математический порядок и получать верные результаты.
Ошибка вычислений и непредсказуемый результат
Одна из основных причин, почему деление на ноль невозможно, заключается в том, что это противоречит самому математическому определению. Если мы возьмем любое число и разделим его на ноль, результат будет бесконечностью или неопределенным. Это противоречит основным принципам математики и логическому мышлению.
Когда программа пытается выполнить деление на ноль, она может вызывать ошибку или просто выдавать непредсказуемый результат, поскольку нет определенного значения, которое можно вернуть. Иногда это может привести к возникновению бесконечного цикла или аварийному завершению программы. Поэтому разработчики программ и математических алгоритмов стараются избегать деления на ноль в своих кодах.
Проблемы в программировании и базах данных
В программировании и базах данных возникает множество проблем, с которыми разработчики и администраторы часто сталкиваются. Некоторые из этих проблем могут быть связаны с ошибками в коде, неправильной архитектурой системы или недостаточным пониманием требований клиента. В этом разделе мы рассмотрим некоторые из наиболее распространенных проблем, с которыми можно столкнуться в программировании и работе с базами данных.
1. Ошибки в коде
Одним из наиболее распространенных типов проблем являются ошибки в коде. Они могут быть вызваны неправильными алгоритмами, некорректными условиями или неправильной работой с данными. Ошибки в коде могут проявляться в виде некорректной работы приложения, неверных результатов или даже полного аварийного завершения программы.
2. Проблемы с производительностью
В работе с базами данных и программировании часто возникают проблемы с производительностью. Это может быть вызвано неправильной оптимизацией запросов к базе данных, медленной работой сети или высокой нагрузкой на сервер. Проблемы с производительностью могут привести к замедлению работы системы, некорректной отдаче данных или даже полной недоступности приложения.
3. Недостаточная безопасность
При разработке программного обеспечения и работе с базами данных безопасность является одним из самых важных аспектов. Недостаточная защита данных, неправильное использование шифрования или неправильная аутентификация пользователей могут привести к серьезным проблемам, таким как утечка конфиденциальной информации или несанкционированный доступ к системе.
4. Проблемы масштабируемости
В работе с базами данных и программировании может возникнуть проблема масштабируемости, то есть способности системы справляться с увеличением объема данных или количества пользователей. Неправильная архитектура системы, ограничения базы данных или неправильная настройка программного обеспечения могут привести к тому, что система не сможет эффективно работать при больших объемах данных или большом количестве пользователей.
5. Проблемы совместимости
При разработке программного обеспечения и работы с базами данных важно учитывать совместимость с различными платформами и операционными системами. Неправильное использование сторонних библиотек или фреймворков, неправильное использование API или неправильное форматирование данных могут привести к проблемам совместимости, когда система может работать некорректно или вообще не запускаться на определенных платформах или операционных системах.
Научное объяснение неразделимости нуля
При делении одного числа на другое, мы ищем ответ на вопрос: «сколько раз можно разделить одно число на другое?». Но в случае с нулем этот вопрос становится бессмысленным. Дело в том, что операция деления определена только для чисел, отличных от нуля. Почему?
Наука объясняет эту запретную операцию с помощью понятия «бесконечность». Когда мы пытаемся разделить ноль на какое-либо число, мы сталкиваемся с ситуацией, когда ответ на вопрос о том, «сколько раз можно разделить ноль на это число», будет бесконечным количеством раз.
Мы можем провести примерную аналогию ситуации, когда мы делаем попытку разделить конкретное количество предметов на ноль. У нас просто не будет возможности сделать это, так как ответ на вопрос о том, сколько раз мы можем разделить эти предметы на ноль, будет неопределенным.
Таким образом, научное объяснение неразделимости нуля заключается в том, что деление на ноль противоречит математическим правилам, определенным для операции деления. Ноль не может быть подвержен делению, так как ответ на такую операцию будет неопределенным и не имеет смысла в рамках математической логики.
Абсурдность попытки разделить ноль
На первый взгляд может показаться, что разделение на ноль должно быть возможно, если мы обладаем достаточно внимания и математических способностей. Однако факт остается фактом: математика строго запрещает деление на ноль, и есть несколько причин, по которым это абсурдно.
Во-первых, деление на ноль приводит к неопределенности. Когда мы делим число на другое число, мы ищем число, которое, умноженное на делитель, дает нам исходное число. Однако когда мы пытаемся разделить на ноль, не существует числа, которое, умноженное на ноль, даст нам любое другое число. Буквально говоря, нет такого числа.
Во-вторых, деление на ноль противоречит основным математическим принципам. В алгебре мы знаем, что если a*b=c, то с:a=b. Если мы попытаемся применить этот принцип к делению на ноль, получим, что любое число деленное на ноль равно любому другому числу. Это спорит с тем, что мы знаем и понимаем о числах.
Наконец, деление на ноль может привести к ошибке или несостоятельности системы. Многие математические модели и алгоритмы используют деление в своих расчетах. Если допустить возможность деления на ноль, это может привести к непредсказуемым и невозможным результатам, что делает систему ненадежной и неполезной.
Таким образом, деление на ноль является абсурдной операцией, которая противоречит основным математическим принципам и приводит к неопределенности. Это не просто ограничение, наложенное математикой, но и необходимость в предотвращении ошибок и сохранении надежности систем.
Вопрос-ответ:
Почему нельзя делить на ноль?
Деление на ноль не определено в математике. Это связано с особенностями числовой системы и множеством делимых чисел.
Что произойдет, если попытаться поделить число на ноль?
Если попытаться поделить число на ноль, то возникнет математическая ошибка. Как правило, программа или калькулятор выдаст ошибку или вернет бесконечность.
Почему нельзя делить на ноль в программировании?
В программировании деление на ноль может привести к ошибке или некорректным результатам. Это связано с особенностями работы компьютера и математическими правилами деления.
Можно ли найти решение уравнения, в котором присутствует деление на ноль?
Нет, нельзя найти решение уравнения, в котором присутствует деление на ноль. Такое уравнение обычно считается некорректным и не имеет смысла вычислений.
Почему деление на ноль является математической ошибкой?
Деление на ноль является математической ошибкой, так как не существует числа, на которое можно было бы разделить любое число и получить определенный результат. Это противоречит математическим законам и правилам.